해시(Hash), 스킵 리스트(Skip list), 세트(Set)

맵 (Map)

맵의 특성

맵: key-value 쌍을 저장하는 자료 구조
key 값에는 중복이 없으며(unique), 각 key는 하나의 entry만을 가짐
search, insert, remove 연산 가능

맵의 활용

대학 정보 시스템
DNS

맵의 구현

단일 연결 리스트 기반 맵의 연산별 최악의 경우 시간 복잡도는 아래와 같다. ($k$: key, $v$: value)

연산	함수	시간 복잡도	설명
탐색	get($k$)	$O(n)$	리스트를 순회하므로 리스트 크기에 비례
삽입	put($k, v$)	$O(n)$	리스트에서 삽입은 $O(1)$이지만 중복 검사 위해 리스트 순회
삭제	remove($k$)	$O(n)$	리스트 순회 후 삭제

탐색과 삭제가 빈번한 경우 맵의 Linear time은 비효율적이므로 다른 방식으로 구현이 필요하다.

$n$개의 아이템이 존재하고, 0에서 $N-1$까지의 정수를 키 값으로 사용하는 맵이 존재한다고 가정하자. (단, $N{\geq}n$)
이 때, 아래 연산들의 시간 복잡도는 $O(1)$의 상수 값을 갖는다.

어떤 아이템, 키 값 쌍이 존재하는지 판단
특정 키 값을 통해 아이템을 반환/수정
특정 키 값으로 새로운 아이템 삽입
특정 키 값으로 아이템 삭제

$n$에 비해 $N$이 매우 클 경우 낭비되는 메모리가 발생하고, 키 값이 정수가 아닌 경우도 존재하기 때문에
다양한 포맷에 대해 맵 구조를 제공할 수 있는 해시 함수(Hash Function)를 도입한다.

해시 (Hash)

해시 테이블에서의 탐색, 삽입, 삭제 연산은 최악의 경우 $O(n)$의 시간 복잡도를 갖는다.
Load factor $\alpha = n / N$는 해시 테이블의 성능에 영향을 준다.

Load factor: 해시 테이블에서 현재 저장된 요소의 수와 전체 슬롯 수(배열 크기)의 비율을 나타내는 지표

해시 값이 랜덤하다고 가정하면, Open addressing 기반 삽입 연산의 탐색횟수는 $\frac{1}{1-\alpha}$이다.

해시 테이블에서 모든 dictionary ADT 작업의 예상 실행 시간은 $O(1)$이며,
load factor가 100%에 가까워지지 않는 한 hash는 매우 빠르다.

해시 함수 (Hash Function)

해시 함수 $h$는 주어진 키 값을 고정된 구간 $[0, N-1]$ 내의 정수로 변환하며, 이 때 $h(x)$를 해시 값이라고 한다.
✨$h(x) = x\,mod\,N$

해시 테이블은 해시 함수 $h$와 크기 $N$의 배열(테이블)로 구성된다.
해시 테이블을 통한 맵 구현의 목표는, 아이템 $(k, v)$를 인덱스 $i=h(k)$에 저장하는 것이다.

$h(x)=x\,mod\,100$일 때, 해시 테이블은 아래와 같다. 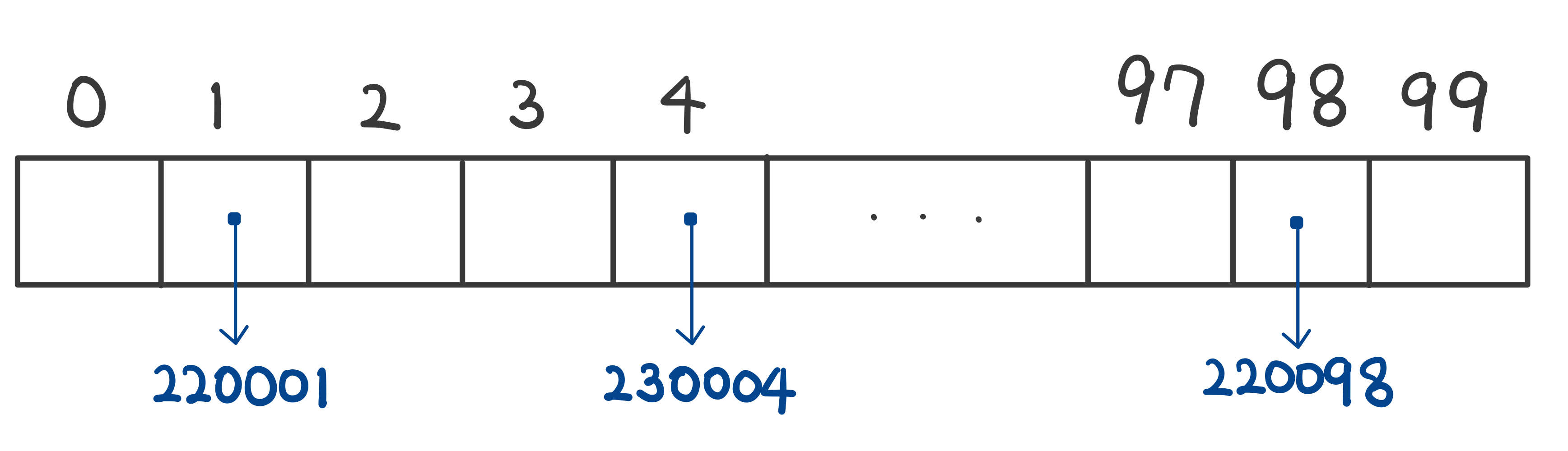$x=220098$의 경우에 이미 해시 값이 저장되어 있는데
추가로 $x=230098$을 저장하려고 하면 해시 값 충돌(Collision)이 발생한다.
그러면 다음 키 값에 연속적으로 저장해도 되지만 키 값이 최대한 산포(scatter)되어 있는 게 좋으므로,
해시 코드(Hash Code) $h_1$과 압축 함수(Compression Function)$h_2$를 조합하여 사용한다.
$h(x) = h_2(h_1(x))$

키 값을 정수(해시 코드)로 변환 후 특정 범위로 압축했다.

해시 코드 (Hash Code)

해시 코드는 해시 함수에 의해 생성된 고정 길이의 값으로, 데이터나 객체를 고유하게 식별하는 역할을 수행한다.

방식	설명
Memory address	메모리 주소, default in JAVA
Integer cast	키의 비트 값들을 숫자로 변환
Component sum	키를 고정된 길이로 분할 후 분할 값 sum
Polynomial accumulation	키의 각 비트별 가중치를 고려 $p(z)=a_0+a_1z+a_2z^2+…+a_{n-1}z^{n-1}$

Horner’s rule 활용하여 $p(z)$를 $O(n)$ 내에 계산 가능
$p_0(z) = a_{n-1},\,\,p_i(z)=a_{n-i-1}+zp_{i-1}(z)\,\,for\,i=1, 2, …, n-1$

해시 충돌 (Collision)

서로 다른 element가 동일한 셀에 맵핑되는 것을 해시 충돌이라고 하며, 해결 방법은 아래와 같다.

방식	설명	장점	단점
Separate Chaining	충돌이 발생한 데이터를 연결 리스트에 추가	간단한 구현, 연결 리스트 동적 관리	테이블 외 별도의 데이터 구조 관리 필요
Open Addressing	해시 테이블 내의 다른 빈 셀을 찾아 데이터를 삽입	해시 테이블 내에서 처리하므로 효율적인 메모리 사용	클러스터링, 삭제 어려움
Linear Probing	순차적으로 다음 셀에 삽입	별도의 메모리 불필요	로컬 충돌 지속, 탐색 시간 길어짐
Double Hashing	부가적인 해시 함수 사용하여 다른 셀에 삽입	분산 균형	복잡한 구현

Linear Probing과 Double Hashing은 Open Addressing의 한 종류이다.

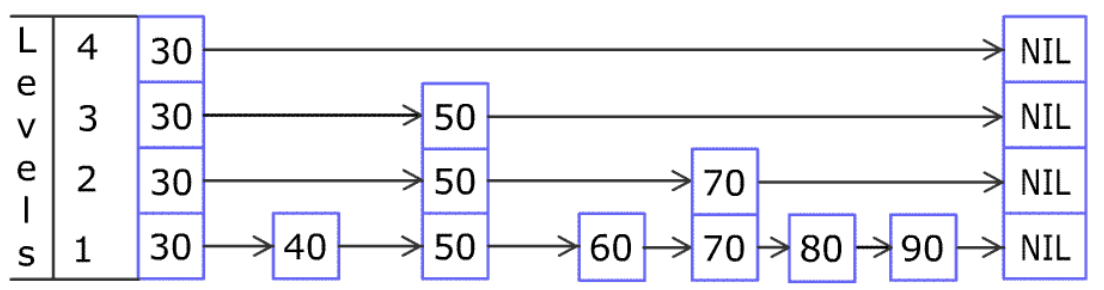
스킵 리스트 (Skip List)

리스트 $S_0, S_1, …, S_h$의 시리즈이다.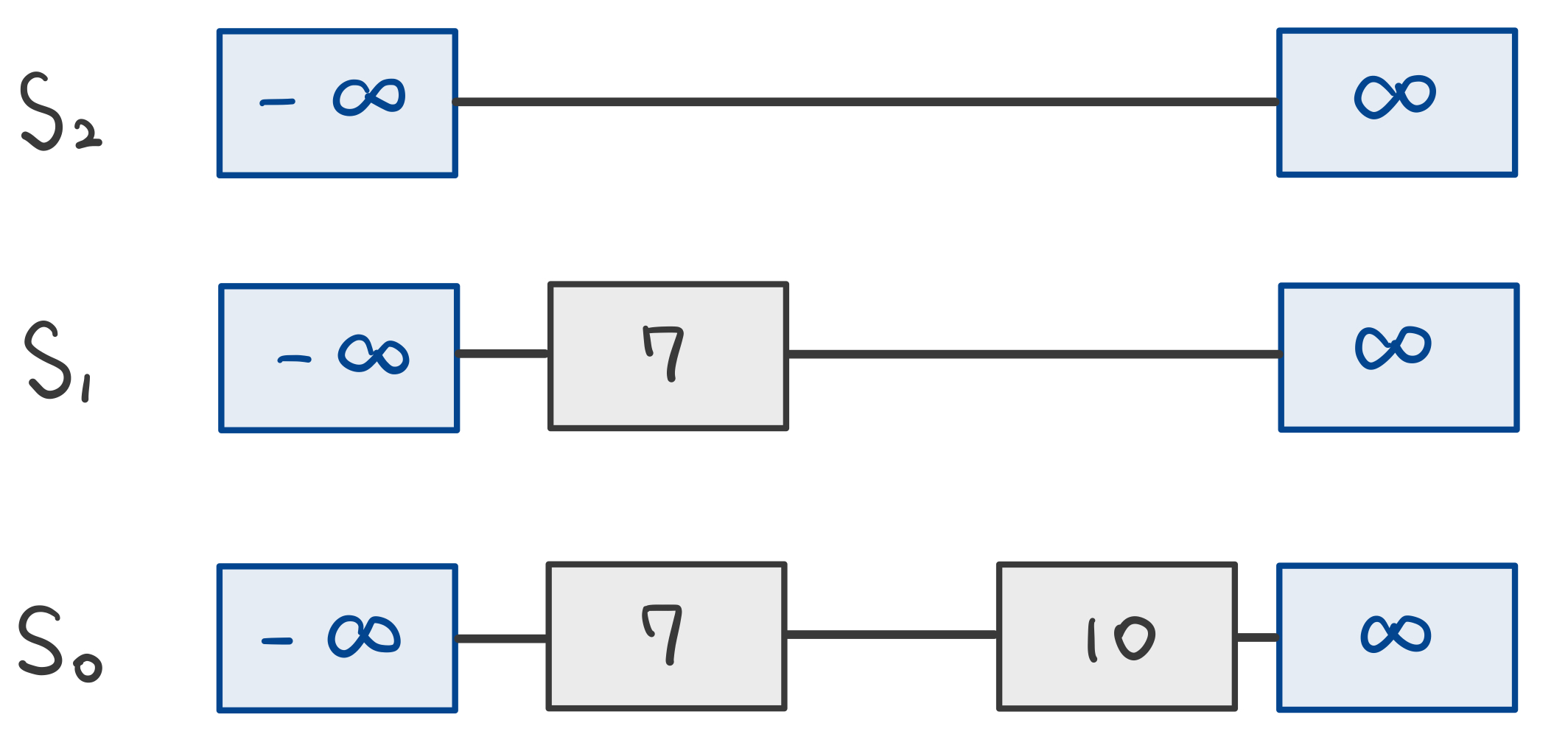

$S_0$→$S_2$로 갈수록 아래 리스트의 부분집합화: $S_0\supseteq S_1\supseteq S_2\supseteq … \supseteq S_h$
$S_0$은 모든 키 값 보유
모든 리스트 $S_i$는 $(-\infty,+\infty)$ 사이의 키 값을 보유 (ASC 정렬)
최상단 $S_h$는 키 값으로 $-\infty, +\infty$만 보유
높이 $h=log\,n$
탐색, 삽입, 삭제의 평균 시간 복잡도는 $O(log\,n)$, 최악의 경우는 $O(n)$

스킵 리스트의 탐색

좌측 상단에서 탐색 시작
탐색값 $x$와 현재 키$y\leftarrow key(next(p))$ 비교
- $x=y$: return $element(next(p))$
- $x>y$: scan forward
- $x<y$: drop down

(예제) Find 70

Level 5 (그림에는 없지만) Level 5의 $-\infty$에서 시작,
$70<next(-\infty)=+\infty$이므로 drop down →현재 키: Level 4 30
Level 4 $70<next(30)=+\infty$이므로 drop down →현재 키: Level 3 30
Level 3 $70>next(30)=50$이므로 scan forward →현재 키: Level 3 50
Level 3 $70>next(50)=+\infty$이므로 drop down →현재 키: Level 2 50
Level 2 $70=next(50)=70$이므로 return $element(next(50))=element(70)$

스킵 리스트의 삽입

$(x, 0)$ 삽입할 위치 탐색
레벨을 결정하기 위해 동전 던지기 수행
동전 앞면이 나오면 새로운 레벨을 추가하고, 해당 레벨에서 삽입 반복
즉, $i\geq h$, 스킵 리스트에 $S_{h+1}, …, S_{i+1}$ 리스트 추가

동전 던지기를 통해 해당 레벨에서 앞으로 진행해야 할지 멈춰야 할지 결정
동전 앞면이 $i$회 나오려면 $i+1$회째에 뒷면이 나온 것이다. → 총 $i+1$회 try

각 리스트 $S_0, S_1, …, S_i$에서 $x$보다 작은 가장 큰 위치 $p_0, p_1, …, p_i$ 탐색
$j \leftarrow 0, 1, …, i$에 대해, $(x, o)$을 리스트 $S_j$의 위치 $p_j$에 삽입

스킵 리스트의 삭제

삭제할 값을 가진 노드 의 위치 $p_0, p_1, …, p_i$ 탐색
리스트 $S_0, S_1, …, S_i$에서 $p_0, p_1, …, p_i$ 삭제
스킵 리스트 성질 만족하도록 리스트 지움 (최상단 리스트는 $-\infty, +\infty$만 포함)

스킵 리스트의 성질

스킵 리스트를 위해 사용되는 공간은 삽입 알고리즘의 각 호출에서 사용되는 난수 비트에 따라 달라진다.
따라서, 스킵 리스트에 사용되는 노드의 개수는 $\sum_{i=0}^{h} {\frac{n}{2^i}} = n\sum_{i=0}^{h} {\frac{1}{2^i}}<2n$ 이며,
이 때의 공간 복잡도는 $O(n)$ 이다.

스킵 리스트의 탐색 시간은 drop-down과 scan-forward 단계를 모두 고려한 값이다.
drop-down은 스킵 리스트의 높이만큼 수행되므로, $O(log\,n)$이다.
동전 던지기를 통해 진행 여부를 결정하므로 scan-forward는 이전 단계의 동전 던지기와 관련이 있다.
각 단계에서의 scan-forward 기댓값은 $1 \times \frac{1}{2} + 2 \times \frac{1}{2^2} + 3 \times \frac{1}{2^3} + … = \sum_{i=1}^{n}i \times \frac{1}{2^i} \leq 2$이고, 시간 복잡도는 $O(log\,n)$이다.
즉, 스킵 리스트의 시간 복잡도는 $O(log\,n)$ 이다.

셋 (Set)

셋과 멀티셋(Multiset)의 특성

셋: 중복을 허용하지 않고 순서가 없는 element 집합
멀티셋: 중복을 허용하며 순서가 없는 element 집합 (맵과 유사하지만, 멀티셋은 키 : 값 매칭이 일 대 다도 가능)

셋의 구현

셋은 리스트(List)를 통해 구현할 수 있다.
리스트를 통해 특정 순서에 따라 정렬되어 저장되며, 이 때 공간 복잡도는 $O(n)$이다.
리스트 기반 셋의 연산별 시간 복잡도는 아래와 같다.

연산	시간 복잡도	설명
탐색	$O(n)$	리스트 순차 탐색
삽입	$O(n)$	리스트에서 삽입은 $O(1)$이지만 중복 검사 위해 리스트 순회
삭제	$O(n)$	리스트 순회 후 삭제

참고

Data Structures and Algorithms in JAVA Fourth Edition (Michael T. Goodrich, Roberto Tamassia)
이미지(skip list): Skip list add element