힙(Heap)이란?
힙의 특성
- Heap-Order: 최댓값/최솟값 탐색에 유리한 반정렬 상태 – 최대 힙: root의 키 값이 최대, $key$(parent)${\geq}key$(child) – 최소 힙: root의 키 값이 최소, $key$(parent)${\leq}key$(child)
- 완전 이진 트리(Complete Binary Tree): 힙의 높이가 $h$일 때, 0, 1, …, $h-1$의 레벨 $i$는 $2^i$개의 노드 보유
- 우선순위 큐(Priority Queue) 구현을 위해 도입 - $(key, element)$
- 이진 탐색 트리와 다르게 중복 값 허용
힙의 활용(우선순위 큐 활용)
- OS 작업 스케쥴링
힙의 구현
배열(Array)를 통한 구현이 일반적이다.
배열은 선언 후 크기를 수정할 수 없다.
어떤 노드의 인덱스가 $i$일 때,
왼쪽 자식 노드의 인덱스: $2i+1$
오른쪽 자식 노드의 인덱스: $2i+2$
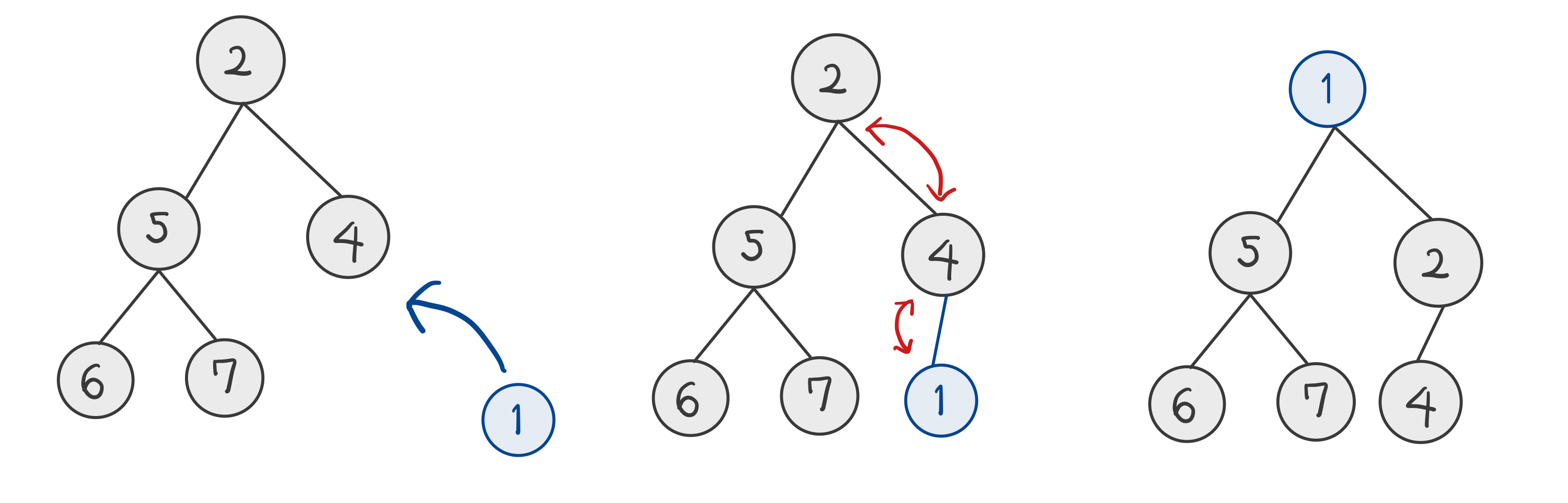
Insertion
Insert a new key at index $n$
- 마지막 노드에 새로운 노드 삽입
- 삽입한 노드의 부모 노드들과 비교/교환하여 힙 순서 유지 - Upheap
→ $O(log\,n)$ : Upheap의 런타임은 힙의 높이의 일부
(참고) 최소 힙에서의 삽입 연산
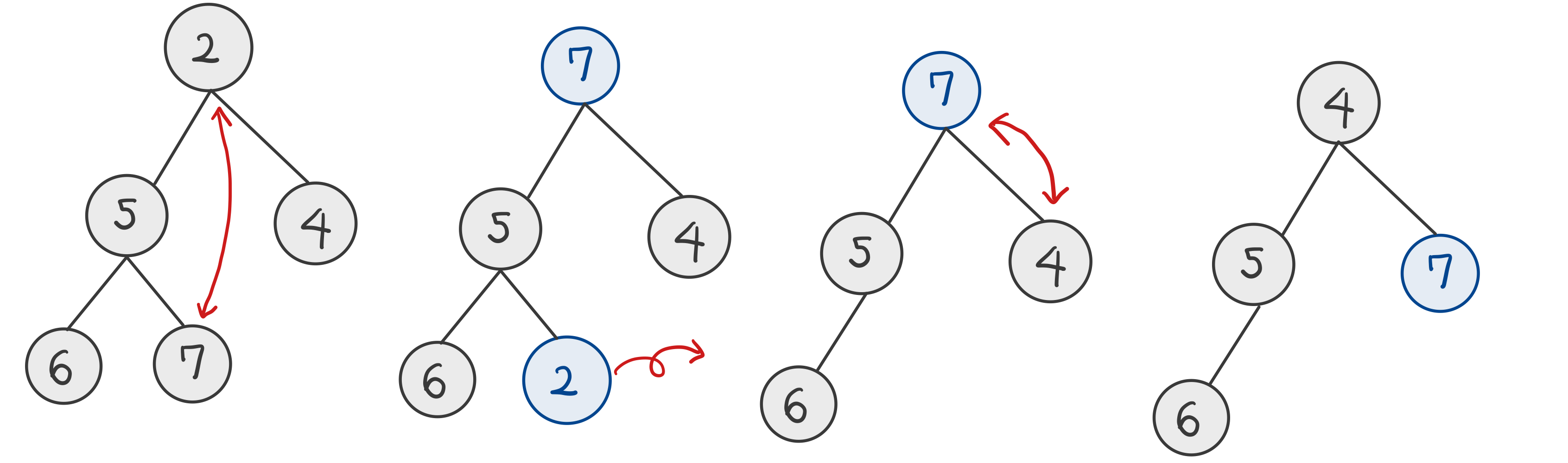
Removal
Remove the key at index $n-1$
- 루트 노드와 마지막 노드 교환
- 마지막 노드(원래 루트 노드) 삭제
- 힙 순서 만족하도록 교환 - Downheap
→ $O(log\,n)$ : Downheap의 런타임도 힙의 높이의 일부
(참고) 최소 힙에서의 삭제 연산
Downheap 과정에서, 자식 노드인 4와 5 중 4가 더 작기 때문에 4와 7을 교환했다.
Merge
2개의 힙 $T_1$, $T_2$와 키 값 $k$가 주어졌을 때,
루트 노드의 키가 $k$이고, $T_1, T_2$를 서브 트리로 갖는 힙을 만들 수 있다.
Downheap을 통해 힙 순서 특성을 유지한다.
- 노드 개수가 $n$으로 동일한 두 트리를 merge할 때의 시간 복잡도: $O(log\,n)$
Bottom-up Heap Construction
$i$번째 단계에서, 각각 ($2^i-1$)개의 키를 갖는 $(n+1)/2^i$개의 elementary heap을 구성할 수 있다.
모든 노드는 적어도 2개의 대체 경로(proxy path)를 순회하기 때문에, 시간 복잡도는 $O(n)$이다. (linear time)
proxy path: go right? go left?
$n$개의 연속적인 삽입 연산($O(nlog\,n)$)을 하는 것보다 Bottom-up Heap이 더 유리하다.
참고
- Data Structures and Algorithms in JAVA Fourth Edition (Michael T. Goodrich, Roberto Tamassia)
- [자료구조] 힙(heap)이란