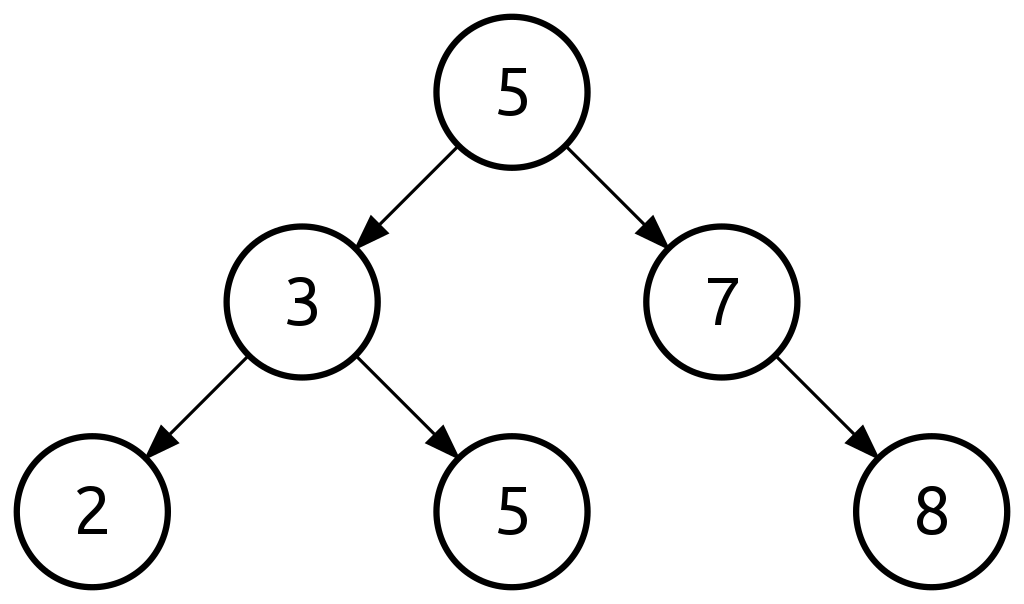
이진 탐색 트리 (Binary Search Tree; BST)
이진 탐색 트리의 특성
순서가 있는(정렬되어 있는) $(key, value)$ 쌍으로 구성된 자료구조를 Ordered Map이라고 한다.
키 값에 의해 데이터가 정렬되어 있기 때문에 탐색/삭제에 유리하다.
Ordered Map의 일반적인 시간 복잡도는 $O(log\,n)$이다.
정렬된 배열을 구현하기 위해 사용하는 Ordered map을 Search Table이라고 한다.
시간 복잡도는 다음과 같다.
| 연산 | 시간 복잡도 | 설명 |
|---|---|---|
| 탐색 | $O(log\,n)$ | 이진 탐색 |
| 삽입 | $O(n)$ | 최악의 경우 삽입할 위치까지 모든 아이템($n/2$개) 이동 |
| 삭제 | $O(n)$ | 최악의 경우 삭제할 위치까지 모든 아이템 이동 |
이진 탐색 트리는 아래 성질을 만족한다.
- 트리의 왼쪽 서브트리에 있는 모든 노드의 값은 현재 노드의 값보다 작다.
- 트리의 오른쪽 서브트리에 있는 모든 노드의 값은 현재 노드의 값보다 크다.
세 노드 $u, v, w$에 대해, $u$가 $v$의 왼쪽 서브 트리이고, $w$가 $v$의 오른쪽 서브 트리일 때,
$key(u)<key(v)<key(w)$
- 중복된 값을 가지는 노드는 허용되지 않습니다. 각 노드는 유일한 키 값을 가진다.
- 외부 노드는 아이템을 저장하지 않는다.
- 중위 순회할 경우 모든 노드를 키의 오름차순으로 방문한다
이진 탐색 트리의 구현
- 삽입 put($k, o$) : 외부 노드에 삽입하려는 키 값 기록하고 내부 노드로 전환
- 삭제 remove($k$),
v는 $k$를 저장하는 노드
–v가 leaf node:v삭제
–v자식 노드 1개:v삭제 후v자리에v의 자식 노드를 붙임
–v자식 노드 2개:v자리에 왼쪽 서브 트리의 최댓값 또는 오른쪽 서브 트리의 최솟값(우선)
- 공간 복잡도: $O(n)$
- 시간 복잡도: $O(h)=O(log\,n)$
skew tree 구성될 때가 최악의 경우로, 높이 $h=n$이 된다.
AVL 트리
AVL 트리의 특성
모든 내부 노드의 자식 노드간 높이 차이가 1 이하인 이진 탐색 트리를 AVL 트리라고 한다.
[Proof] 노드 수가 $n$인 AVL 트리의 높이는 $O(log\,n)$임을 증명하라.
높이가 $h$인 AVL 트리의 최소 내부 노드 수를 $n(h)$라고 하자.
[Basis] $n(1)=1$, $n(2)=2$
[Case for $h>2$] 좌/우 서브 트리 모두 최소 노드 수를 갖는 AVL 트리여야 전체 AVL 트리의 노드 수도 최소일 것이다. 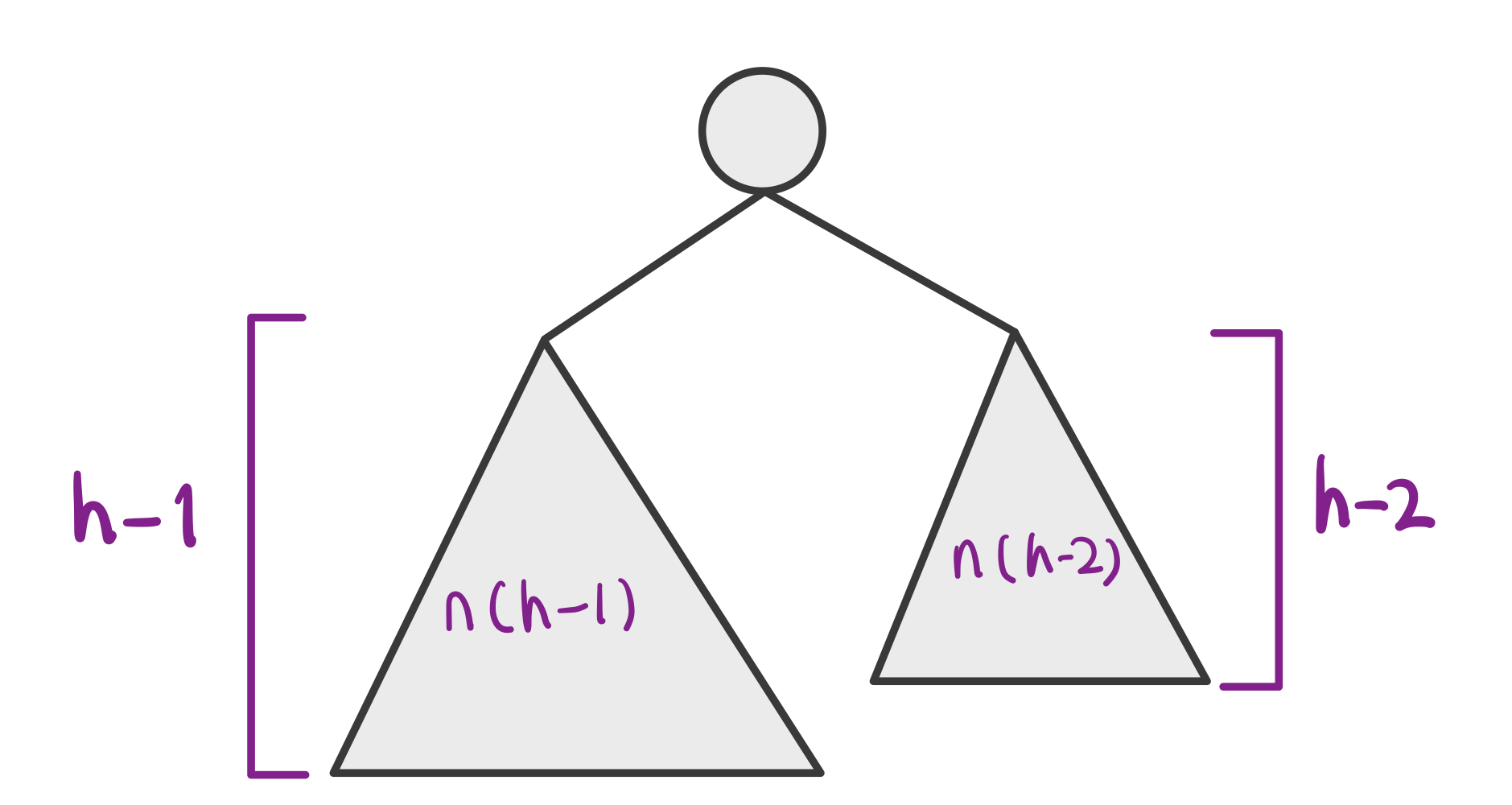
$n(h)=1+n(h-1)+n(h-2)$인데, $n(h-1)>n(h-2)$이고 $n(h)>2n(h-2)$이므로
$n(h)>2n(h-2),\,n(h)>4n(h-4),\,n(h)>8n(h-8),…$, 즉, $n(h)>2^in(h-2i)$이다.
$i=\frac{h}{2}-1 \,\Rightarrow \,n(h)>2^{\frac{h}{2}-1} \,\Rightarrow\, h<2log\,n(h)+2$
AVL 트리의 구현
AVL 트리의 삽입/삭제 연산은 BST와 동일한 방식으로 수행 후 Trinode Restructuring을 통해 리밸런싱을 진행한다.
노드가 (root) A-B-C (leaf) 순서일 경우, 트리 불균형을 해결하는 방법은 다음과 같다.
- LL: Left 서브 트리의 Left 자식에 삽입/삭제가 발생한 경우,
A에서 Right 회전 수행 - LR: Left 서브 트리의 Right 자식에 삽입/삭제가 발생한 경우,
BLeft →ARight 회전 수행 - RR: Right 서브 트리의 Right 자식에 삽입/삭제가 발생한 경우,
A에서 Left 회전 수행 - RL: Right 서브 트리의 Left 자식에 삽입/삭제가 발생한 경우,
BRight →ALeft 회전 수행
Right/Left 회전의 pseudo code는 각각 아래와 같다.
1
2
3
4
5
6
7
8
9
10
11
Right_Rotation(node): // 시계 방향
// Right 회전 수행
new_root = node.left // node=A의 왼쪽 자식인 B를 new_root로 설정
node.left = new_root.right // B의 오른쪽 서브 트리를 A의 왼쪽 서브 트리로 이동 > A 자식이 3개가 됨
new_root.right = node // A를 B의 오른쪽 서브 트리로 변경 > A-B 부모-자식 관계 뒤바뀌면서 A 자식은 2개가 됨
// 회전 후 높이 갱신
node.height = max(height(node.left), height(node.right)) + 1
new_root.height = max(height(new_root.left), height(new_root.right)) + 1
return new_root
1
2
3
4
5
6
7
8
9
10
11
Left_Rotation(node): // 반시계 방향
// Left 회전 수행
new_root = node.right // node=A의 오른쪽 자식인 B를 new_root로 설정
node.right = new_root.left // B의 왼쪽 서브 트리를 A의 오른쪽 서브 트리로 이동 > A 자식이 3개가 됨
new_root.left = node // A를 B의 왼쪽 서브 트리로 변경
// 회전 후 높이 갱신
node.height = max(height(node.left), height(node.right)) + 1
new_root.height = max(height(new_root.left), height(new_root.right)) + 1
return new_root
참고
- Data Structures and Algorithms in JAVA Fourth Edition (Michael T. Goodrich, Roberto Tamassia)
- 이미지(binary search tree): DSA binary search tree
- 이미지(AVL tree): AVL tree
- C AVL 트리(AVL Tree) 설명
- AVL 트리를 알아보자